The Monty Hall Paradox

The Monty Hall Paradox or (The Monty Hall Problem) is a brain teaser, in the form of a probability puzzle. In the puzzle there are 3 doors. The host (Monty Hall of the Let's Made A Deal TV program for 30 years) tells you that behind one of the doors there is a new car. Behind the other two doors are goats. You can pick a door and win whatever is behind it. You make your pick, and then Monty open one of the doors that you didn't pick and shows you it contains a goat. He now offers you a chance to switch your choice to the other door that you didn't pick. Should you?
Well, it turns out you really should! This is not intuitive at all. Most people think it does not make any difference - staying or switching both have the same probability of winning the car - 50%. But this is wrong! The actual odds of winning the car if you do not switch in 33.3% and the odds of winning the car if you do switch is 66.7%. The fact that your odds of winning the car are doubled by switching is paradoxical.
I could understand the math steps when this was explained, but it never made intuitive sense to me. So I decided to investigate. I wrote a little C language program to simulate the process and ran millions of simulations. Indeed the odds of winning the car if you do not switch in 33.3% and the odds of winning the car if you do switch is 66.7%! And after some time fooling around with this paradox, now it all does make intuitive sense to me.
Anyhow, I spiffed up the program from the initial bare-bones version I used to confirm the odds and you can play with it you want. It is a Windows command line program written in very simple C that could easily be ported to Unix/Linux or even MacOS. The source code is here. You can download the source code and executable from here. There is also now an exploration of the Monty Hall Paradox with More Doors. Below is the help message:
This program runs simulations of the Monty Hall Paradox,
for info, see https://en.wikipedia.org/wiki/Monty_Hall_problem
Half of the simulations are Keep 1st choice, half are Switch.
Output is a running tally of Wins and Loses for both Keep and Switch.
Usage: montyhall {a|k|s} {#simulations}
where a = alternate between keep & switch each time (default)
k = run all keep simulations 1st, then all switch
s = run all switch simulations 1st, then all keep
where #simulations >= 200 and <= 10 million (default=2000)
with half Keep original choice and half Switch choice.
Note: { } are optional args and | means choose only one.
Examples:
C:>montyhall -> alternate keep & switch each of 2000 times
C:>montyhall k -> 1000 keep followed by 1000 switch
C:>montyhall s 20000 -> 10000 switch followed by 10000 keep
C:>montyhall 2000000 -> alternate keep & switch 2 million times
C:>montyhall ? -> print this message and exit.
If output is redirected to a file, the file contains additional info
and fewer running tallies are displayed.
(However redirecting to nul produces no output at all).
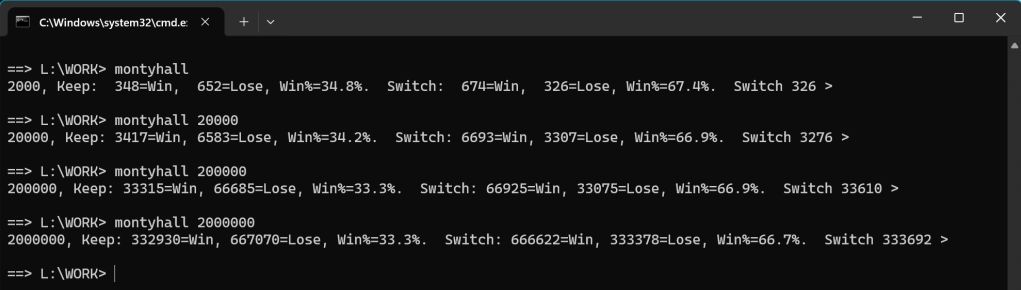
Here is some sample output:
Monty Hall Paradox with More Doors
The very interesting history of this paradox
View C source code
Download C source code (right click)
Download both the source code and the executable (zip file)
| Back to Leigh's Home Page | Site Map | Site Search |